Helper Functions
In class we discussed in addition to the stereotypical recursive
patterns in the book, the ``helper function with something extra''
pattern. This is a page of notes about that.
Reverse
Let's say we want to define a function rev that takes a
list and returns that list with the words in reverse order.
For example:
(rev '(aye bee sea)) ; (sea bee aye)
(rev '(ex)) ; (ex)
(rev '()) ; ()
-
Here's a cute but (albeit probably inefficient) way to do this using
higher order functions:
(define rev
(lambda (lis)
(accumulate (lambda (x y) (append y x))
(map list lis))))
but let's say we want to do it recursively.
-
A straightforward thought is to take the reverse of the list
with it's car removed, and then put that first element on at
the end.
(define rev
(lambda (lis)
(if (null? lis)
'()
(append (rev (cdr lis))
(list (car lis))))))
Let's look at a call graph for (rev '(a b c d)), to make sure
we understand how it works.
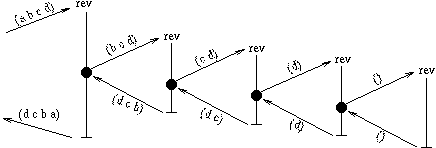
That's nice, but maybe inefficient, because it is expensive to tack
things onto the end of a list but cheap to tack them onto the
front.
-
We can use a ``helper function with something extra'' instead. The
helper function will take two arguments: a list to go at the end
of its result, and a list to be reversed and put at the
beginning. For example:
(rev-aux '(aye bee sea) '(one two three)) ; (three two one aye bee sea)
So let's define it:
(define rev
(lambda (lis)
(rev-aux '() lis)))
(define rev-aux
(lambda (end-of-result to-be-reversed)
(if (null? to-be-reversed)
end-of-result
(rev-aux (cons (car to-be-reversed)
end-of-result)
(cdr to-be-reversed)))))
This should be efficient because it only calls quick little functions
like car and cons, rather than append,
which takes time proportional to the length of its first argument.
Let's look at a call graph of (rev '(a b c d)), to see if we
can understand this.
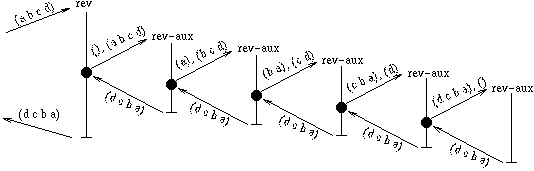
Parallel Prefix
Consider the function pp, which is supposed to compute the
``parallel prefix'' of a list. Eg if the function it is passed is
+ then it computes the running totals, as follows:
For example:
(pp + '(1 1 1 1 1)) ; (1 2 3 4 5)
(pp + '(1000 200 30 4)) ; (1000 1200 1230 1234)
(pp + '(14)) ; (14)
(pp + '()) ; ()
As with most problems, there are a bunch of different strategies we
might use here.
- Simple recursion: cut off the car, figure out the parallel
prefix of the rest, and modify it to give the right answer.
(define pp
(lambda (f lis)
(if (null? lis)
'()
(let ((fir (car lis)))
(cons fir
(map (lambda (x) (f x fir))
(pp f (cdr lis))))))))
This looks nice, except one might worry about efficiency, in that
shared partial sums are not being used. The computation of the
next-to-last element is completely separate from the computation of
the last element.
-
Instead we can try to do it from the other direction, recursing by
removing the last element:
(define pp
(lambda (f lis)
(define butlast (lambda (lis) (reverse (cdr (reverse lis)))))
(define last (lambda (lis) (car (reverse lis))))
(cond ((null? lis) '())
((null? (cdr lis)) lis)
(else (let ((partial-pre (pp f (butlast lis))))
(append partial-pre
(list (f (last lis)
(last partial-pre)))))))))
This seems elegant, in that it uses the already-computed total for the
first part of the list in calculating the remaining part, so it will
not more calls to f than necessary. But it will be
inefficient for a different reason: car is fast, while
butlast takes time of order the length of the list, as does
the call to append.
-
In an attempt to have our cake and eat it too, we can define
pp in term of a recursive helper function, which takes an
extra argument: the running total so far.
(define pp
(lambda (f lis)
(if (null? lis)
'()
(cons (car lis)
(pp-aux f (car lis) (cdr lis))))))
(define pp-aux
(lambda (f running-total lis)
(if (null? lis)
'()
(let ((new-running-total (f running-total (car lis))))
(cons new-running-total
(pp-aux f
new-running-total
(cdr lis)))))))
Which is efficient both in its manipulation of the list and in
taking advantage of the left-to-right structure of the accumulation of
the results.
Let's look at it's call graph for (pp + '(0 1000 200 30 4))
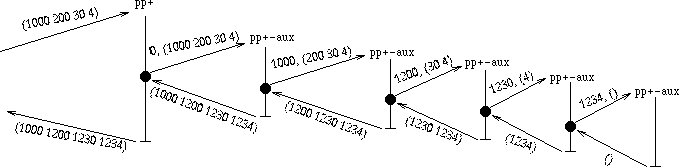
The Fibonacci Sequence
Another problem we can use helper functions for is the Fibonacci
function discussed in the text. (We all know where the Fibonacci
sequence comes from: it's the number of female rabbits you have each
year, if you buy a female rabbit the car year, each litter contains
one female rabbit, there is one litter a year, rabbits live for two
years, and there is no shortage of male rabbits. The Fibonacci
sequence also comes up in spiral growth patterns, like the whorls in a
sunflower.)
Each element in the sequence is the sum of the previous two elements:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, etc.
We want to define our function such that
(fibb 0) ; 0
(fibb 1) ; 1
(fibb 2) ; 1
(fibb 3) ; 2
(fibb 4) ; 3
(fibb 5) ; 5
(fibb 6) ; 8
(fibb 7) ; 13
(fibb 8) ; 21
(fibb 9) ; 34
The obvious recursive definition is:
(define fibb
(lambda (n)
(cond ((= n 0) 0)
((= n 1) 1)
(else (+ (fibb (- n 1)) (fibb (- n 2)))))))
This will be very inefficient for large arguments, because Scheme will
calculate the same Fibonacci numbers over and over many times. In
fact the total number of recursive calls is going up exponentially
with the argument! We can see that by sketching the call graph of
(fibb 9)
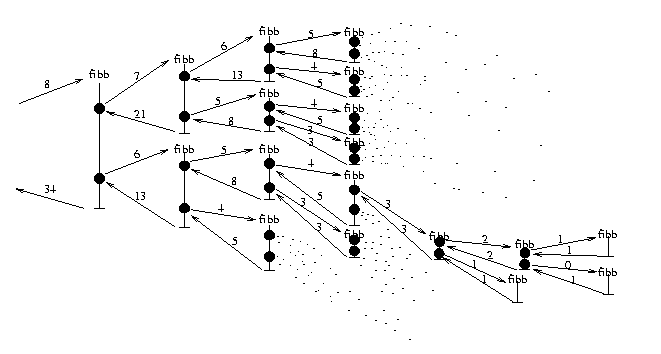 If you think about it, you'll see that the function either recurses
with two calls to itself or returns 1. So the total number of calls
to fibb when you go (fibb n) must be twice the
returned result minus one. This grows pretty quickly.
If you think about it, you'll see that the function either recurses
with two calls to itself or returns 1. So the total number of calls
to fibb when you go (fibb n) must be twice the
returned result minus one. This grows pretty quickly.
Instead we would like to sum things up as we would if we were doing
this by hand. Doing it by hand, we would keep track of the previous
two Fibonacci numbers to calculate the next one, and repeat that until
we get up to where we want to be.
This can be done with a helper function that takes three arguments:
the cdr two Fibonacci numbers, and the number of steps that remain to
be taken.
(define fibb
(lambda (n)
(fibb-aux 0 1 (- n 1))))
(define fibb-aux
(lambda (fibb-nm1 fibb-n steps-remaining)
(cond ((= steps-remaining 0) fibb-n)
((= steps-remaining -1) fibb-nm1)
(else (fibb-aux fibb-n
(+ fibb-nm1 fibb-n)
(- steps-remaining 1))))))
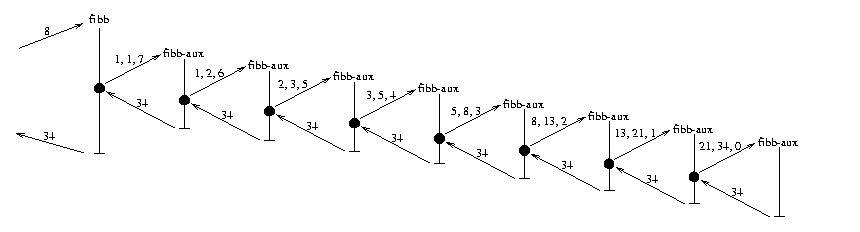
This gives a much faster algorithm, as seen from the following call
graph for (fibb 9)
Barak Pearlmutter <bap@cs.unm.edu>


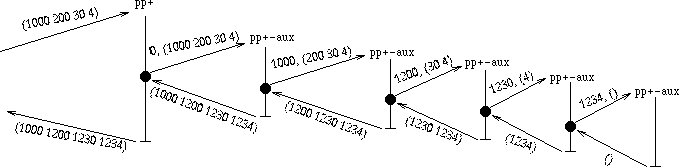
 If you think about it, you'll see that the function either recurses
with two calls to itself or returns 1. So the total number of calls
to fibb when you go (fibb n) must be twice the
returned result minus one. This grows pretty quickly.
If you think about it, you'll see that the function either recurses
with two calls to itself or returns 1. So the total number of calls
to fibb when you go (fibb n) must be twice the
returned result minus one. This grows pretty quickly.
